遗传算法
因为在之前就有了解过该算法,并且该算法在好多工具都有体现,所以也刚好有个机会,去整理整理相关的资料,以后也会不断的去充实的!
1.遗传算法定义
首先,我们先讲个例子。例如,在一群小狗里面挑选优秀的警犬种子。
(1)设定好小狗的初始群大小;
(2)定义一个函数来区分优秀犬类和普通犬类;
(3)我们选择出优秀犬类,并让他们繁殖自己的后代;
(4)最后,这些后代替代原来狗群中的普通类,不断地充实优秀犬类的占比,并且最后不断的重复该过程。
遗传算法的工作过程其实也是这样的,在某种程度上模拟进化的过程,所以我们可以由此得出该算法的定义;
遗传算法(Genetic Algorithm)是一类借鉴生物界的进化规律(适者生存,优胜劣汰遗传机制)演化而来的随机化搜索方法;
2.遗传算法的实现细节
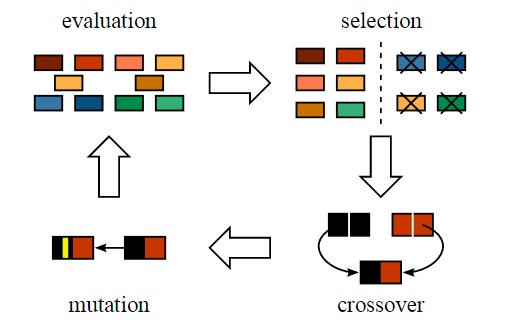
总体的实现过程如图:
首先,算法随机生成一定数量的个体,有时候操作者也可以干预这个随机产生过程,以提高初始种群的质量。在每一代中,都会评价每一个体,并通过计算适应度函数得到适应度数值。按照适应度排序种群个体,适应度高的在前面。这里的“高”是相对于初始的种群的低适应度而言。
下一步则是产生下一代个体并且组成种群,而这个过程则是通过选择和繁殖来完成的,即Crossover交叉操作和Mutation变异。然后再进行根据新个体的适应度进行,但同时不意味着完全以适应度高低为导向,因为单纯选择适应度高的个体将可能导致算法快速收敛到局部最优解而非全局最优解,我们称之为早熟。作为折中,遗传算法依据原则:适应度越高,被选择的机会越高,而适应度低的,被选择的机会就低。初始的数据可以通过这样的选择过程来不断进行来组成一个相对优化的群体。
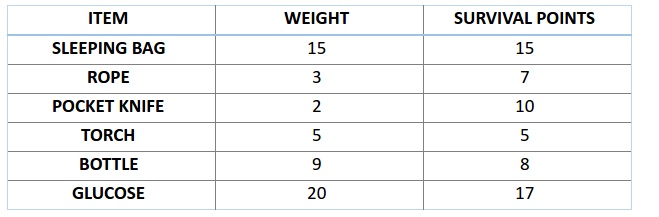
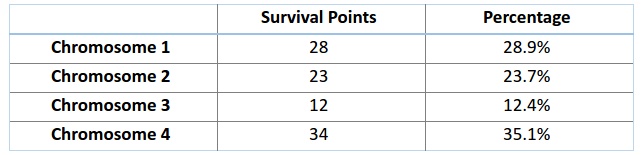
在该过程中具体的实现细节,我们以背包问题为例:比如,你准备要去野游 1 个月,但是你只能背一个限重 30 公斤的背包。现在你有不同的必需物品,它们每一个都有自己的「生存点数」(具体在下表中已给出)。因此,你的目标是在有限的背包重量下,最大化你的「生存点数」。
2.1初始化
如上流程所述,我们首先来初始化定义总体,总体包含各个个体,而每个个体都有一套属于自己的染色体。
染色体可表达为 2 进制数串,在这个问题中,1 代表接下来位置的基因存在,0 意味着丢失。(特定位置上的基因代表了上方背包问题表格中的物品,比如第一个位置上是 Sleeping Bag,那么此时反映在染色体的『基因』位置就是该染色体的第一个『基因』。)
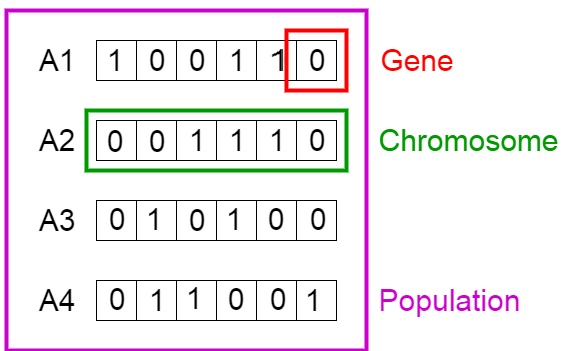
如上图,我们将图中的 4 条染色体看作我们的总体初始值。
2.2适应度函数
接下来,我们计算前两条染色体的适应度分数。对于 A1 染色体 [100110] 而言, 则有
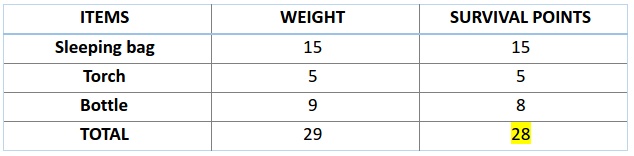
类似的,则对于A2 染色体 [001110] 来说 :
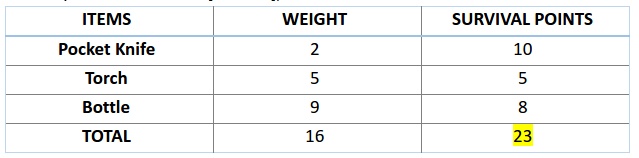
一次类推,当染色体包含更多生存分数时,也就意味着它的适应性更强。因此,由图可知,染色体 1 适应性强于染色体 2。
2.3选择
现在接下来我们依照步骤二从总体中选择适合的染色体进行交叉操作,并且产生自己的下一代,但是这样将会导致染色体在几代之后相互差异减小,失去了多样性。故而,这部分会有多种选择算法,常见的选择操作主要有以下几种 :
a)轮盘赌选择 。选择某假设的概率是通过这个假设的适应度与当前群体中其他成员的适应度的比值而得到。此方法是基于概率选择的,存在统计误差,因此可以结合最优保存策略以保证当前适应度最优的个体能够进化到下一代而不被遗传操作的随机性破坏,保证算法的收敛性。
b)排序选择。对个体适应值取正值或负值以及个体适应度之间的数值差异程度无特殊要求 , 对群体中的所有个体按其适应度大小进行排序,根据排序来分配各个体被选中的概率。
c)最优个体保存。父代群体中的最优个体直接进入子代群体中。该方法可保证在遗传过程中所得到的个体不会被交叉和变异操作所破坏,它是遗传算法收敛性的一个重要保证条件 ;它也容易使得局部最优个体不易被淘汰,从而使算法的全局搜索能力变强。
d)随机联赛选择。每次选取N个个体中适应度最高的个体遗传到下一代 群体中。具体操作如下: 从群体中随机选取N个个体进行适应度大小比较,将其中适应度最高的个体遗传到下一代群体中;将上述过程重复执行M(为群体大小)次,则可得到下一代群体。
而我们一般会进行轮盘赌选择法, 想象有一个轮盘,现在我们将它分割成 m 个部分,这里的 m 代表我们总体中染色体的个数。每条染色体在轮盘上占有的区域面积将根据适应度分数成比例表达出来。
如图:Chromosome1的百分比:28/(28+23+12+34)=28.9%
我们基于上面的百分比来建立轮盘,如下图所示:
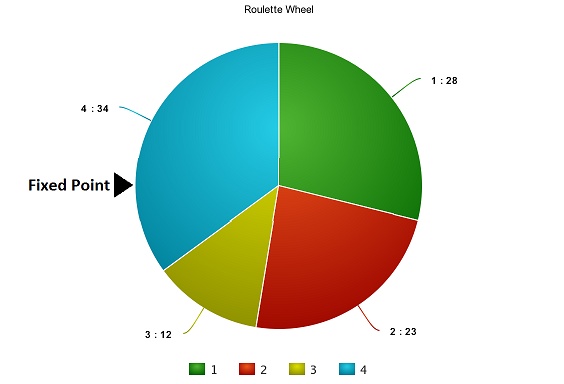
现在,这个轮盘开始旋转,我们将被图中固定的指针(fixed point)指到的那片区域选为第一个亲本。然后,对于第二个亲本,我们进行同样的操作。有时候我们也会在途中标注两个固定指针,如下图:
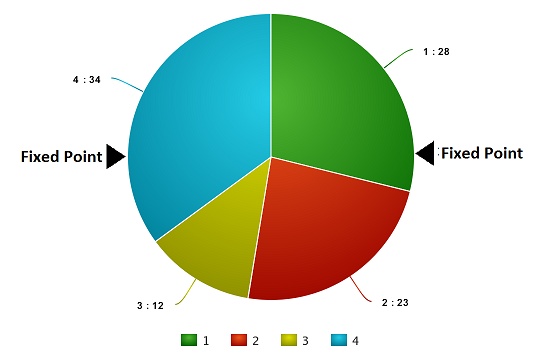
通过这种方法,我们可以在一轮中就获得两个亲本。我们将这种方法成为「随机普遍选择法」(Stochastic Universal Selection method)。
2.4交叉
在上一个步骤中,我们已经选择出了可以产生后代的亲本染色体。现在我们来对染色体 1 和 4(在上一个步骤中选出来的)进行交叉操作 ,而此处的常用交叉算法有如下几种:
a)单点交叉。 在个体编码串中随机设置一个交叉点后在该点相互交换两个配对个体的部分基因 。
b)两点交叉。 在相互配对的两个个体编码串中随机设置两个交叉点,并交换两个交叉点之间的部分基因 。
c)均匀交叉。 两个相互配对个体的每一位基因都以相同的概率进行交换,从而形成两个新个体。
d)算术交叉。 由两个个体的线性组合而产生出新的个体。
此处我们来演示单点交叉于多点交叉:
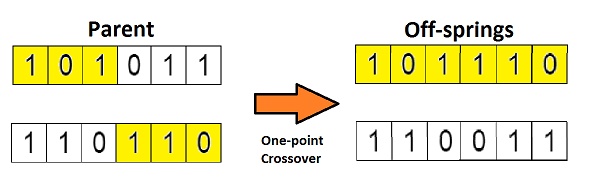
这是交叉最基本的形式,我们称其为「单点交叉」。这里我们随机选择一个交叉点,然后,将交叉点前后的染色体部分进行染色体间的交叉对调,于是就产生了新的后代。
如果你设置两个交叉点,那么这种方法被成为「多点交叉」,见下图:
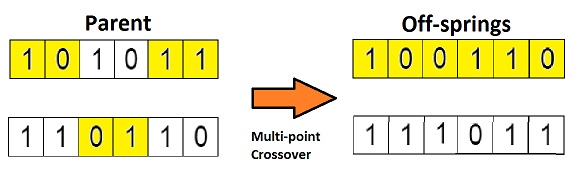
2.5变异
如果现在我们从生物学的角度来看这个问题,那么请问:由上述过程产生的后代是否有和其父母一样的性状呢?答案是否。在后代的生长过程中,它们体内的基因会发生一些变化,使得它们与父母不同。这个过程我们称为变异,它可以被定义为染色体上发生的随机变化,正是因为变异,种群中才会存在多样性。
下图为变异的一个简单示例:

变异完成之后,我们就得到了新为个体,进化也就完成了,整个过程如下图:
在进行完一轮遗传变异之后,我们用适应度函数对这些新的后代进行验证,如果函数判定它们适应度足够,那么就会用它们从总体中替代掉那些适应度不够的染色体。这里有个问题,我们最终应该以什么标准来判断后代达到了最佳适应度水平呢?
一般来说,有如下几个终止条件:
- 进化次数限制;
- 计算耗费的资源限制(例如计算时间、计算占用的内存等);
- 一个个体已经满足最优值的条件,即最优值已经找到;
- 适应度已经达到饱和,继续进化不会产生适应度更好的个体;
- 人为干预;
- 以及以上两种或更多种的组合。
参考文献
【1】https://zhuanlan.zhihu.com/p/28328304【例子】
【2】https://zh.wikipedia.org/wiki/%E9%81%97%E4%BC%A0%E7%AE%97%E6%B3%95